Wyświetlenie artykułów z etykietą: głebokie uczenie

W poniższym artykule (i dołączonym do niego filmie) wykażę bezsensowność używania głębokiego uczenia (ang. Deep Learning), sieci neuronowych (ang. neural network) do rozpoznawania obrazów na przykładzie rozpoznawania pisma odręcznego ze zbioru znaków MNIST i udowodnię to w praktyce.

Wykażę także, że do rozpoznawania odręcznie pisanych cyfr czy szerzej obrazu, nie jest konieczne uczenie systemu dziesiątkami tysięcy próbek, a wystarczy jedna lub najwyżej kilka, a dodatkowo nie będzie miało znaczenia jakiej wielkości jest próbka służąca do uczenia systemu, jak i próbka do badania jego skuteczności. Nie będzie też miało znaczenia wyśrodkowanie, wielkość, kąt obrotu, czy grubość pisanych linii, co ma kapitalne znaczenie w metodach rozpoznawania obrazu opartych na uczeniu maszynowym czy deep learning.

Jak wiemy, każdy obraz w komputerze składa się z pojedynczych punktów (Max Planck mówi że cały nasz świat składa się z pikseli), które połączone w odpowiedni sposób tworzą obraz. Tak samo jest ze znakami tworzącymi cyfry w bazie danych znaków MNIST.

Zbiór znaków MNIST i jego klasyfikacja jest swego rodzaju abecadłem dla każdego początkującego studenta czy osoby rozpoczynającej zabawę z głębokim uczeniem czy sieciami neuronowymi.
Zbiór ten został skompletowany przez Yann’a Lecun (http://yann.lecun.com/exdb/mnist/) i zawiera 70.000 obrazów w rozdzielczości 28x28 pikseli w 255 odcieniach szarości. Przyjęto, że 60.000 obiektów stanowi zbiór treningowy, a 10.000 są to elementy ze zbioru testowego.  Obraz (w tym wypadku cyfra od 0 do 9) reprezentowany jest jako macierz 2D o wymiarach 28×28, w której wartości 0-255 reprezentują odcień szarości piksela. Łatwiejszą formą do przetwarzania przez algorytmy uczenia maszynowego jest postać wektora, którą otrzymujemy odczytując wartości pikseli z obrazu wiersz po wierszu. Stąd otrzymamy 784-wymiarowy wektor (28*28=784) reprezentujący jeden obrazek z cyfrą. Z tego wynika, że cały zbiór treningowy to macierz o wymiarach 60000×784.

Teraz tylko wystarczy użyć dostępnych w chmurze narzędzi typu TensorFlow, pobrać kilka plików w Pythonie, poczytać o wielu mądrych metodach uczenia sieci, kupić o tym kilka książek, albo po prostu pobrać gotowca co robi większość i stworzyć swoją pierwszą sieć neuronową.
Wow, do jednego znaku składającego się z 28 linii po 28 punktów specjalnie przygotowanego do rozpoznawania, czyli odpowiednio wycentrowanego, wyskalowanego w idealnej rozdzielczości tęgie głowy wymyśliły, że skoro nasz ludzki mózg składający się z neuronów potrafi to odczytać to stworzymy mini elektroniczny mózg ze sztucznych neuronów to on też to odczyta. I udało się! Wyniki są prawie idealne, bliskie 100%, ale…

Używanie sieci neuronowych do rozpoznawania cyfr to jak zastąpienie patyka służącego do pisania cyfr na piasku na plaży wyspecjalizowanym robotem wybierającym z plaży po jednym ziarnku piasku w celu otrzymania tego samego wzoru!

Czy myślicie że nasz mózg patrząc na cyfrę tnie ją na paski, piksele, wektory i analizuje punkt po punkcie? Jeżeli przyjmiemy wyliczenia dr. Clarka, że rozdzielczość naszego wzroku to 576 megapikseli (tak naprawdę nie więcej niż 20 megapikseli w centrum patrzenia), to naprawdę nie ma takiego napoju energetycznego, który wspomoże nasz mózg w takiej pracy.

Co więcej, czy na tym ma polegać uczenie? Czy my musimy zobaczyć 60.000 znaków, aby się ich nauczyć, czy może nauczycielka w szkole podstawowej napisała go raz i kazała zapamiętać?
Czy jeżeli narysuje Wam jeden raz pewien znak np.:

to rozpoznacie ten poniżej jako inny?



Oczywiście jest troszkę inny, ale gdy obok niego mamy określony zbiór np. cyfr i ten znak  - to każdy ten znak rozpozna mimo że widzi go pierwszy raz. Nie będzie też miał problemów z jego narysowaniem po chwili w innym miejscu.

I teraz najważniejsze, jak zapamiętujemy ten znak? Piksel po pikselu, 784 punkty? A co jakby to był znak w rozdzielczości 256 na 256 punktów, czyli takiej jaką ma zwykła ikonka na naszym domowym komputerze składający się z 65536 punktów?
Nie, nasz mózg jest wspaniały jeżeli chodzi o upraszczanie wszelkich danych jakie do niego dochodzą, a tym bardziej jak to są tak ogromne dane, jak dane o obrazie.

Pomyślmy przez chwilę jak słowami opisalibyśmy ten znak komuś innemu, a otrzymamy od razu  jedną z metod uproszczonego zapamiętywania – pewnie opiszemy to mniej więcej tak:
dwa odcinki, poziomy i pionowy, pierwszy odcinek jest poziomy, a na jego końcu pod kątem 90 stopni styka się z odcinkiem pionowym. Zauważmy, że do opisu znaku wystarczą w tym przypadku praktycznie 4 informacje , a nie informacja o 784 punktach w 255 odcieniach szarości. Co więcej tak zapisana informacja jest niezależna od wielkości znaku.

Dokładnie takiej samej metody możemy użyć do zapamiętywania każdego znaku, cyfry, ale i przedmiotu na obrazie niezależnie od tego czy przedmiot będzie w przestrzeni dwu czy trójwymiarowej (w dużym uproszczeniu, gdyż rozpoznawanie obrazu w przestrzeni 2D czy nawet 3D wymaga dokonania dodatkowych czynności – jeżeli to kogoś zainteresuje chętnie opiszę pewne metody łatwego rozpoznawania w kolejny m artykule).

To jeszcze raz, na czym polega ta prosta metoda?

Zapamiętujemy:
1. „punkty startu”
2. „kąt startu”
3. „typ odcinka”
4. „kąt wygięcia odcinka”
5.„kąt połączenia odcinka”

Jak widać wg. mnie mózg ludzki zapamiętuje podstawowe kształty i sposób ich połączenia.
Wykrywamy łatwo linie proste, koła, łuki mniej lub bardziej wygięte i ich wzajemne położenie czy połączenie.

Zobaczmy na przykładzie cyfry 6 (polecam też zobaczyć wszystko na dołączonym filmie https://youtu.be/do9PM2PtW0M):

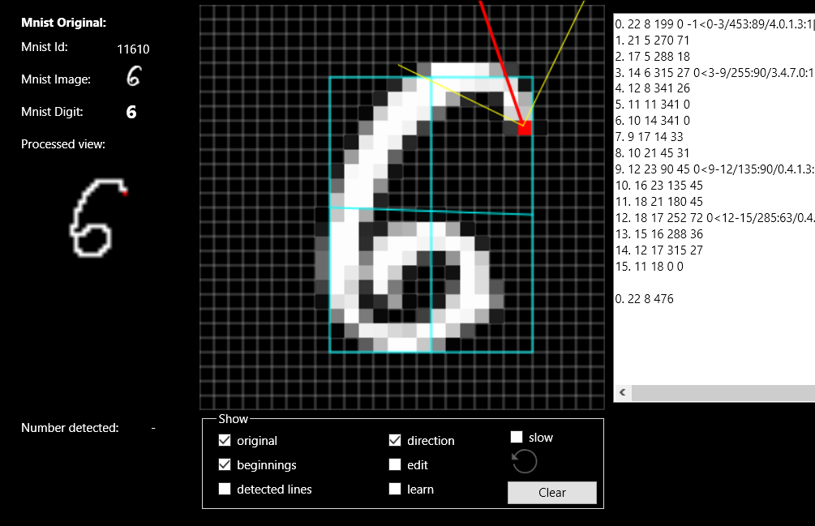
Cyfrę 6 możemy rozpoznać na kilka sposobów - tak naprawdę składa się z kilku odcinków połączonych ze sobą zawsze pod dodatnim kątem, albo z kilku odcinków tworzących na dole koło, albo z jednego odcinka tworzącego swoistego ślimaka, w tym wypadku zakreślającego 476 stopni od początku na górze do końca na dole.

Taka metoda ma też dodatkową zaletę, nie ma znaczenia czy obraz jest obrócony o praktycznie dowolny kąt, nie ma znaczenia grubość linii, nie ma znaczenia wielkość obrazu czy jego położenie, czyli wszystko to co wpływa bardzo negatywnie przy metodach głębokiego uczenia.
Przecież ten sam znak narysowany pod kątem 45 stopni ma wszystkie opisane powyżej parametry takie same.
Uważny czytelnik pewnie od razu wychwyci, a co z cyfrą 6 i 9? – no do pewnego kąta cyfra 6 jest szóstką, a pod pewnym kątem jest już dziewiątką.

Zobaczcie na dołączonym filmie, jak wielkie problemy w rozpoznawaniu mają standardowe metody oparte na głębokim uczeniu, gdy napiszemy cyfry pod kątem. Pamiętajmy też, że zestaw znaków MNIST jest już specjalnie przygotowany, znaki są odpowiednio wyskalowane, wycentrowane, zawsze w identycznej rozdzielczości 28x28 itd.

W tym miejscu sprawniejsi programiści zwrócą pewnie uwagę na jeden wielki problem.

Ludzki mózg widzi po prostu całość, cały obraz, linie, koła – to proste, ale komputer widzi w jednym momencie właściwie tylko jeden punkt, jeden z tych 784 punktów więc jak to oprogramować, jak wykryć te linie? Dodatkowym problemem jest to że niektóre cyfry są pisane grubą czcionką więc gdy widzimy jeden punkt, a obok niego sprawdzamy wszędzie są też zamalowane punkty to skąd wiadomo w którą stronę jest linia?

 (tak widzi komputer) 

Możemy użyć w przypadku znaków dwóch technik:
1. Proste odchudzanie, aż otrzymamy linię grubości punktu (punkt to może być piksel, ale też mogą to być 4 piksele, w zależności od potrzeb)

2. „Metoda szybkiego wtrysku” – wyobrażamy sobie, że musimy zamalować daną cyfrę kolorem (taka funkcja fill) wpuszczamy w jednym punkcie farbę i patrzymy gdzie może się rozprzestrzenić, ale jakby była pod ciśnieniem więc np. w cyfrze 8 na skrzyżowaniu nie rozlewa się na wszystkie strony tylko przelatuje na przeciwną stronę „skrzyżowania” i leci dalej.

Po odchudzeniu gdy mamy już jedną linię, łatwo wyodrębniamy proste, krzywe, kąty i to zapamiętujemy.

Samą metodę obmyśliłem ponad 20 lat temu, przed napisaniem tego artykułu postanowiłem napisać prosty programik sprawdzający czy miałem rację. Po kilku dniach otrzymałem program, nie doskonały bo nie robię przecież programu komercyjnego, ale wystraczający do potwierdzenia, że to działa i ma wykrywalność znaków ponad 97%, a pewnie jakbym jeszcze kilka dni popracował doszedłbym i do 99%.

Z drugiej strony można powiedzieć, że przecież metody opisywane wszędzie w internecie te wykorzystujące sieci neuronowe robią z taką samą wykrywalnością, więc po co robić inaczej? – tak i nie – ta metoda nie wymaga uczenia, super komputerów, nie musi być to zestaw tylko 10 znaków, może ich być dowolna ilość, nie muszą być znaki w formacie 28x28 bo mogą być w 450x725, a właściwie każdy znak może być w dowolnym, za każdym razem innym formacie, znaki mogą być obracane. Dodanie kolejnych znaków nie wymaga ponownego uczenia sieci, nie ma problemu żeby też taki algorytm rozpoznawał dodatkowo znaki wydrukowane w prawie dowolnych czcionkach dostępnych na komputerze oczywiście bez potrzeby jakiegokolwiek dodatkowego ich uczenia.

Niektórzy pewnie napiszą mi zaraz, że tak naprawdę chodzi tylko o pokazaniu na MNIST sposobu uczenia sieci neuronowych, ale nie mogę się z tym zgodzić, to naprawdę nie ma sensu. Nie uczymy się przecież na zajęciach ZPT przybijania gwoździ kulą do rozbiórek domów.
Zostawcie już te znaki bo do tego nie ma kompletnie sensu używania takich metod.

Wywalcie te wszystkie grube książki o Deep Learning, zostawcie to super narzędzie w chmurach, usiądźcie do zwykłego obmyślania coraz lepszych algorytmów sami, takie abecadło programisty.

Do napisania tego artykułu zostałem zmuszony, gdyż podczas pracy nad naszym projektem silnej sztucznej inteligencji SaraAI.com jestem ciągle zasypywany pytaniami jakich używam metod głębokiego uczenia, jakich metod NLP, itd. – a gdy odpowiadam że nie używam bezpośrednio praktycznie żadnych znanych metod widzę tylko zdziwienie i powątpiewanie na twarzach rozmówców, dlatego chciałem wykazać, że nie zawsze musimy trzymać się ogólnie przyjętej linii rozwiązywania problemów programistycznych, możemy zrobić coś zupełnie inaczej otrzymując dużo lepsze wyniki.

Do artykułu polecam też w komplecie film typu "proof of concept": https://youtu.be/do9PM2PtW0M

Mały komentarz:
"Wywalcie te wszystkie grube książki o Deep Learning" - po tych słowach mam nadzieję, że wiecie już, że artykuł specjalnie jest napisany w mocno prowokacyjnym stylu, bo co jak nie emocje doprowadza do wzmożonej dyskusji :-) (nie wyrzucajcie tych książek!)
Nie chodzi mi o porzucenie Deep Learningu, ale o zwrócenie uwagi na to, aby używać tych metod tam gdzie jest to optymalne. Dodatkowo uważam, że dane wrzucane do uczenia należy wstępnie przygotować tak jak to robi nasz mózg.
Nasz mózg wprawdzie odbiera obraz z oka złożony z pikseli (fotonów), ale zanim go porówna z wzorcem pamięciowym przetwarza go i przygotowuje w korze wzrokowej w obszarach V1-V5 - róbmy podobnie.

Zwróćcie uwagę, że jeżeli się wczytacie bardziej, to nie chodzi zupełnie o zestaw znaków MNIST. W tej metodzie mogę dodać dowolną ilość znaków łącznie z wszystkimi chińskimi i nie zmieni to rozpoznawalności - zobaczcie na filmie jak dodaję do cyfr 2 i 3 cyfry II i III rzymskie, co kompletnie nie ma znaczenia w takiej metodzie, (dodaję raz i są rozpoznawane jak 2 i 3 arabskie), a ma duże znaczenie przy metodach opartych na sieciach neuronowych.
Potraktujcie tę metodę jako podstawowe ABC, które rozwijając można bez problemu używać do rozpoznawania twarzy, czy zbioru Fashion MNIST, a także ImageNet.

Jednym z zarzutów jest to, że robiłem ten program kilka dni, a przecież można to zrobić na sieciach w 10 minut. OK, ktoś TensorFlow też nie pisał 10 minut. Teraz gdy mam gotowy algorytm, mogę dodać w kilka minut kolejne alfabety.

"Ale istnieje few-shot learning (czy zero-shot learning), gdzie nie musimy uczyć na 60.000 próbek" - tak, ale metody te na razie mają totalnie niezadowalające wyniki, więc po co, skoro tu mamy prosty i działający algorytm wymagający jednej lub kilku próbek.

"Ale stosuje się augmentację danych (obroty o niewielki kąt, skalowanie, rozszerzanie, wydłużanie)" - tak, ale to tylko powiększenie liczby próbek o kolejne tysiące.

"Wynik 97%, który podajesz nie ma żadnej wymiernej wartości, bo nikt poza tobą nie może tego przetestować." - o to chodzi, że teraz już każdy może uzyskać taki wynik, bo podałem całą metodę, więc dobry programista bez problemu nie tylko powtórzy ten wynik, ale i bez problemu go poprawi.

"Czemu używać Twojego algorytmu, a nie sieci neuronowych?"
Z ciekawości zapytam tylko, bo nie zrobiłem aż tak dużego researchu, czy znacie jakiś program/algorytm, który rozpoznaje dowolne znaki dowolnego alfabetu pisane i drukowane w dowolnym formacie, wielkości, kolorze czy grubości, albo na którym można przeprowadzić taki test:

1 osoba rysuje dowolny znak, może być wymyślony
10 innych osób pisze ten sam znak albo trochę inny
system ma za zadanie stwierdzić kto napisał zły znak.
Dla utrudnienia każdy rysuje znak na tablecie w innej rozdzielczości, z inna grubością pędzla, różnymi kolorami, pod różnymi kątami?

Dodatkowo ten algorytm zadziała na "kalkulatorze" bez dostępu do sieci, dodanie kolejnych obrazów nie wymaga ponownego uczenia całej bazy, wykorzystywane zasoby są naprawdę pomijalnie małe.